機械設計

ねじり応力計算はなぜ、せん断で考えるのか～図解で説明～

本サイトは運営のためにアフィリエイト広告を利用しています。

ねじり応力計算は材料力学の中でも最後に学ぶ単元であり、それまでに覚えたことの応用的な考え方をします。

だから避けてきた人も多いのではないでしょうか。

ねじり応力は基本的にせん断応力として考えてOKです。

トルクの式は曲げモーメントの式と似ています。

今回の参考文献はこちら↓↓です。もっと詳しく知りたい方はぜひ！


せん断応力について

下図は中実軸にねじり荷重がかかっている状態です。

左図は概形図　　　　　右図は平面図
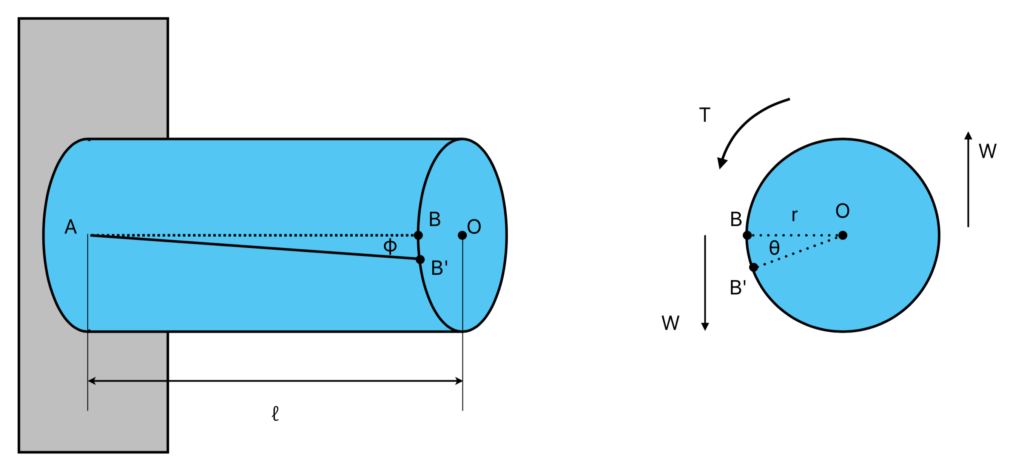
  • ｒ ：半径 [mm]
  • θ ：ねじれ角 [rad]
  • Φ ：せん断角 [rad]
  • ℓ ：軸の長さ [mm]
  • W ：外力 [N]

トルクTは力×腕の長さなので

Ｔ＝Ｗ×ｒ [Nmm]

弧BB'は、弧の長さBB'＝2πr×θ°/360より

θ＝θ°×π/180を変形した、θ°＝θ×180/πを代入すると、下式が得られます。

ＢＢ'＝rθ [mm]

次に、ねじりの力がかかるとせん断応力がなぜ発生するのか解説します。

下図にイメージを示します。

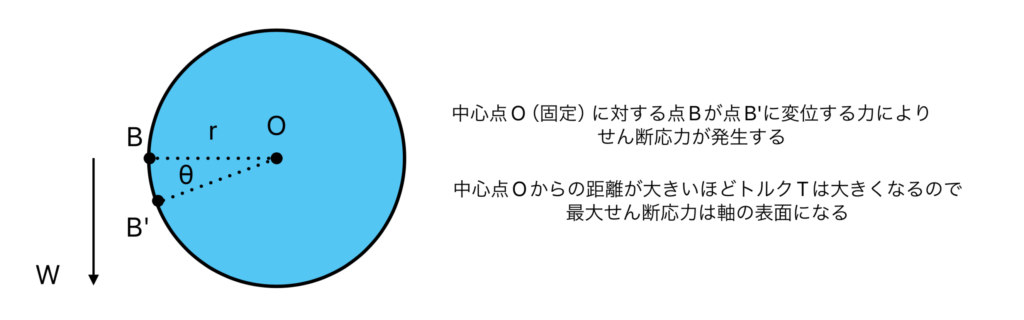
下図のように通常のせん断の時に置き換えて考えるとわかりやすいです。

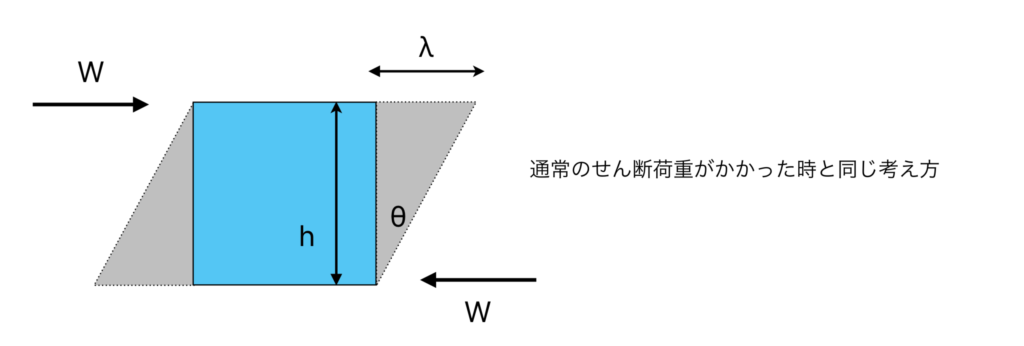
せん断応力τは横弾性係数Gを使用して下式の通りでしたね。

τ＝Gγ
※γはせん断ひずみ

せん断ひずみは通常のせん断荷重がかかった時と同じように考えると下式の通りになります。

γ＝λ/h （λ＝BB'＝rθ、h＝r）

したがって、下式が得られます。

τ = Grθ/ℓ

つまり、せん断応力τは中心からの距離に比例します。

このせん断応力をねじり応力と呼んでいます。

断面二次極モーメントIp・極断面係数Zpについて

まず、断面二次極モーメントIpについてです。

軸心に関する断面二次モーメントと言えます。

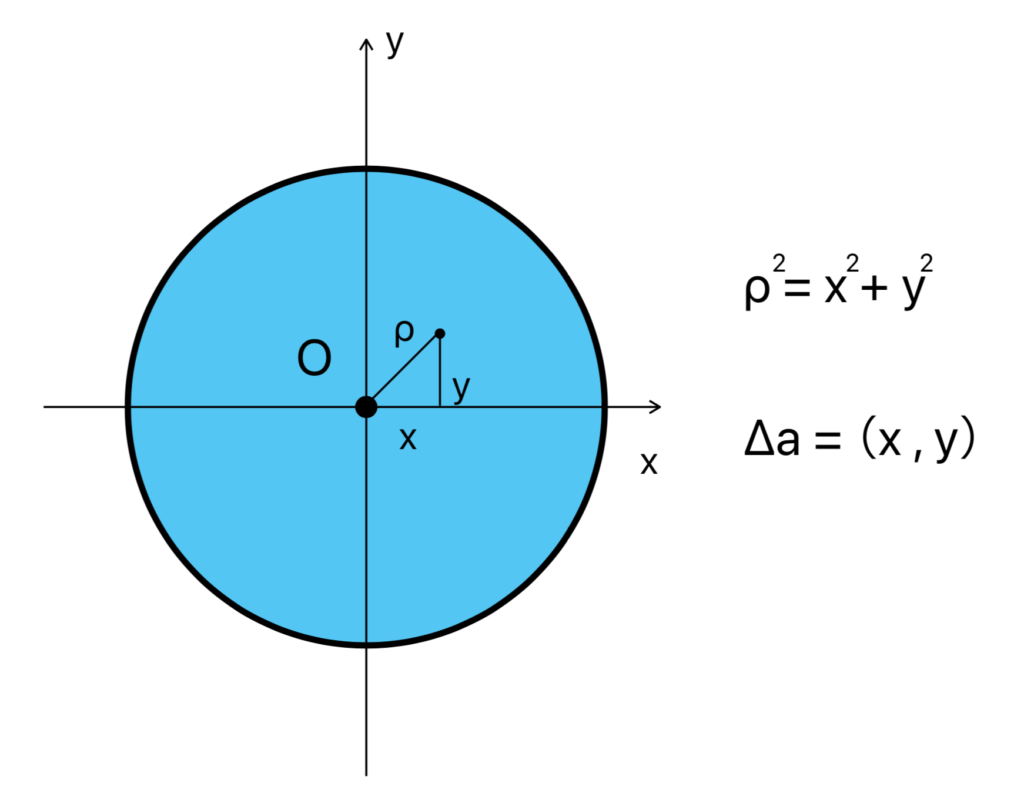
断面二次極モーメントIpは下式で定義されています。（導出の詳細は本に記述ありますのでここでは省略します）

Ip = Σρ2Δa

上式をxとyで表すと

Ip = Σ(x2+y2)Δa
    = Σx2Δa+Σy2Δa
    = Ix＋Iy               ∵Σx2Δa = Ix , Σy2Δa = Iy

このとき、断面が中実円なら Ix=Iyなので

Ip = 2I
    = 2×πd4/64            ∵ I = πd4/64 （I：中実円の断面二次モーメント）
    = πd4/32

次に極断面係数Zpについて、下式で定義されます。

Zp = Ip/r     （r：半径）             ∵Z = I/e （Z：断面係数、e：中立面からの距離）と同様の考え方

断面が中実円ならば

Zp = 2Ip/d
　  = 2πd4/(32×d)
     = πd3/16

となります。

ねじりの基本式

ここまでくれば、ねじりの基本式が登場できます。

T = τZp

変形すると

τ = T/Zp

このようにして、許容せん断応力τと形状から最大トルクを求めたり、形状と作用させるトルクから使用できるかどうか確かめたりできます。

おまけ

ねじり応力τの値は、約90N/mm2で検討しますが、軸は起動時や停止時に大きなトルクが作用するので許容ねじり応力は低くとる方が良いでしょう。

また、ねじれ角についてもある角度以上になると色々な不都合が生じるので、θ＝0.25°/mとしている。（機械設計製図便覧より）

実務では公式さえ使えれば良いですが、式の成り立ちや導出方法を知っていればいざ問題に直面した時に応用して考えることができます。

なにより、信頼できる技術者だと思われるでしょう。

また、当サイトやネット上の情報だけでは不十分なのでぜひ本を手にとって、理解を深めることをお勧めします。

機械設計の会社員にオススメの本はこちらで紹介しています。

他にも機械設計に役立つ情報をこちらでまとめていますのでよかったらご参照ください。

もし内容が役に立ったと思って頂けたらTwitterやブログ、Instagramなどで共有していただければとてもうれしく思います！

今後ともよろしくお願いします。

  • この記事を書いた人

Lancer

機械設計のサラリーマン。 ロボット工学部→土木施工管理→機械設計。 家庭と仕事の両立のために働き方の改善をしようと日々奮闘中。 仕事と子育てに役立つ情報＆趣味の英語を発信しています！！

-機械設計
-