巻上機のワイヤーを選定するときに必ず必要になる計算。それが地巻・層毎のワイヤー長さ計算です。
ワイヤーの長さを選定をする前に以下の条件を決定しておいてください。（仮でもOKです）
- 巻上機ドラム幅 W [mm]
- 巻上機ドラム径 D [mm]
- ワイヤー径 d [mm]
ワイヤーの径の選定方法はこちら
目次
前提条件
平ドラムでの計算となります。
地巻
平ドラムは1層目を地巻とします。
地巻（ぢまき）は最大巻き下げ時でもワイヤー１層目は出ていかないようにすることです。
１層目のワイヤーの溝に２層目のワイヤーを添わせることで乱巻きを防止します。
フリートアングル
下図のように、「巻上機ドラムフランジの内側」と「一番近いシーブのセンター」のなす角が1.5°以内（クレーン構造規格は2°以内）になるようにしなければならないので、これを考慮します。
巻上機と一番近いシーブの最短距離は上記の式で決定できます。
計算の順序
ここに、決定している条件を下記に仮定します。
- 巻上機ドラム幅 W = 900 [mm]
- 巻上機ドラム径 D ＝ 1800 [mm]
- ワイヤー径 d ＝ 32 [mm]
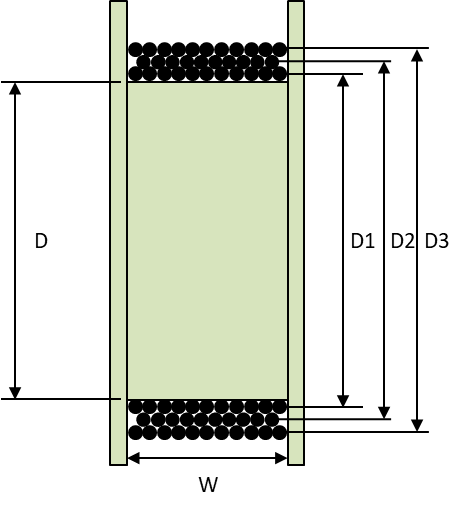
ワイヤー各層の径を求める
まず、ワイヤー1層目の径D1を求めます。
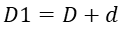
次に、 ワイヤー2層目の径D2を求めます。
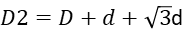
2層目がこうなる理由は下図の通りです。
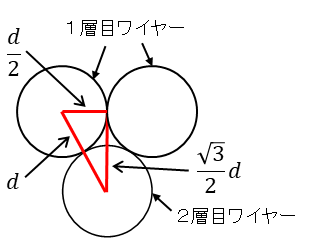
2層目のワイヤーは１層目ワイヤーの間に入る形になります。
すると上図のような配置になり、三角形の比１：２：√３より求めることができます。
同様に考えると、3層目の径D3は下式となります。
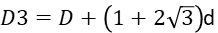
これを一般化すると下記の式が得られます。
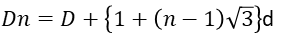
ワイヤーの列数を求める
まずは地巻（1層目）ワイヤー列数を計算します。
1層目ワイヤーの列数は、単純にドラム幅をワイヤー径×製造誤差で割ったものです。
2層目ワイヤーは、1層目ワイヤーの間に配置されるので1層目の列数より1列少ない数字になります。
以降も同様に、奇数層目は地巻と同じ列数で、偶数層目は奇数層目より１列少ない列数になります。
今回の場合は（η：1.05とした）
奇数層：26.7＝26列 （W=900mm ，d=32mm）
偶数層：25列
となります。
ワイヤー先端までの長さを決める
フリートアングルを考慮し、先端までのワイヤー長さを求めます。
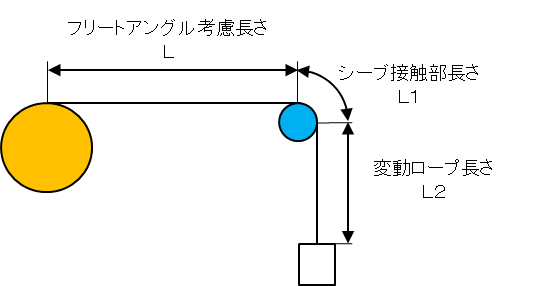
Ｌ，Ｌ１は固定の長さです。
Ｌ２だけは変動するので最大の時の長さＬ２Maxを使用します。
計算例
ワイヤーは2層目まで使用するとします。
1層目径D1 = 1800+32 ＝ 1832mm
2層目径D2 = 1800+32+55.4 = 1887.4mm
1層目列数 C1= 900/(1.05×32) = 26列
よって、1層目のワイヤー長さ ℓ1 は1832×π×26＝149.564m
2層目列数C2 = C1-1 = 25列
よって 、2層目のワイヤー長さ ℓ2 は1887.4×π×25＝148.208m
フリートアングル考慮最小距離 L = 900/(2×tan1.5°) = 17184.8mm
シーブ接触長さ L1 = 628mm とする。
変動ロープ長さ L2 は最大30000mm とする。
ここで、巻上機2層目のワイヤーから引き出されるワイヤー長は30mなので、２層目ワイヤーの最小列数は30000/(1887.4×π) = 5列となる。
よって、すべてのワイヤー長を足すと下記のようになる。
ℓ1+D2×π×5+L+L1+L2 = 226009mm
余裕代を見て230m分購入すれば良いことが分かります。
最後に
もし少しでもお役に立てたならうれしいです！
理屈を知ると”覚える”というより”理解”になるのでより記憶に定着することが皆さんの実体験でもわかると思います。
参考図書はこちらです↓↓
他のも機械設計に役立つ情報をこちらでまとめていますのでよかったらご参照ください。
もし内容が役に立ったと思って頂けたらTwitterやブログ、Instagramなどで共有していただければとてもうれしく思います！
今後ともよろしくお願いします。
